
Z-distributed (normally distributed, e.g.Our critical value calculator supports statistics which are either: Then you need to know the shape of the error distribution of the statistic of interest (not to be mistaken with the distribution of the underlying data!). For example, 95% significance results in a probability of 100%-95% = 5% = 0.05. If you know the significance level in percentages, simply subtract it from 100%.

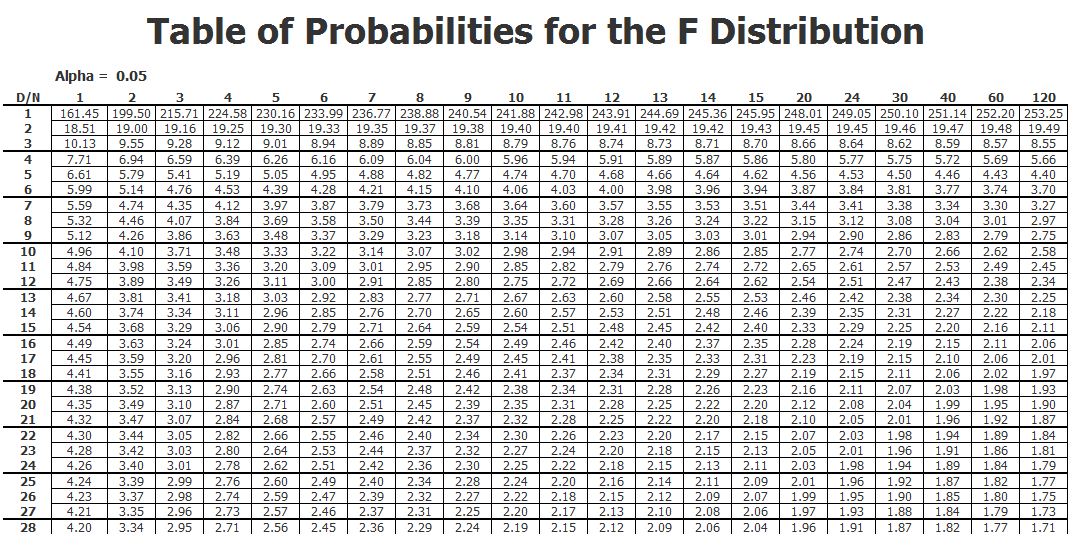
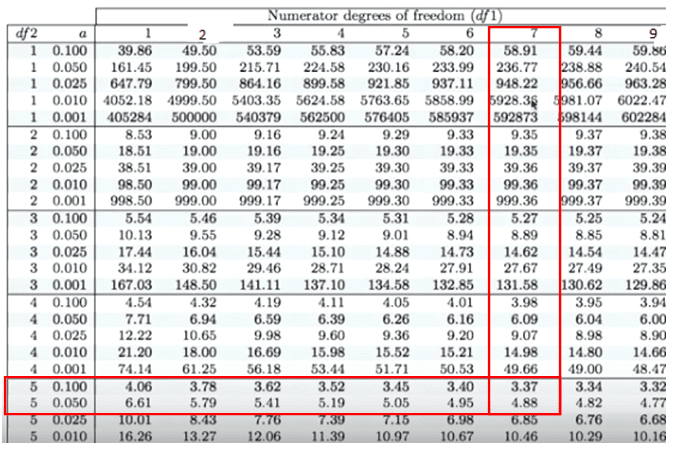
You need to know the desired error probability ( p-value threshold, common values are 0.05, 0.01, 0.001) corresponding to the significance level of the test. significance test, statistical significance test), determining the value of the test statistic corresponding to the desired significance level is necessary. Let me know in the comments if you have any questions on F test calculator for two variances with examples and your thought on this article.If you want to perform a statistical test of significance (a.k.a. To learn more about other hypothesis testing problems, hypothesis testing calculators and step by step procedure, please refer to the following tutorials:
#Calculator f distribution how to
You also learned about the step by step procedure to apply F-test for testing two population variances and how to use F-test calculator for testing two population variances to get the value of test statistic, p-value, and F-critical value. In this tutorial, you learned the about how to solve numerical examples on F-test for testing two population variances. There is enough evidence to support the claim that the populations of the two brands have the same voltage variations. Mathematics Major Statistics Major Sample size $n_1= 13$ $n_2=10$ Sample variance $s_1^2 = 45$ $s_2^2 = 35.5$ Step 1 Hypothesis testing problem Let $X$ denote the final exam scores of students taking the mathematics major and $Y$ denote the final exam scores of students taking the statistics major. Random samples of 13 mathematics majors and 10 statistics majors are selected from the his large class, and the following results are computed based on the final exam scores:Īt the 0.05 level of significance, is there evidence to support the professor's claim? Solution Step 7 - Calculate F critical value Example -1 F test Calculator for two variancesĪ professor from a graduate school claims that there is less variability in the final exam scores of students taking the statistics major than the students taking the mathematics major. Step 6 - Calculate p value from f statistics Step 4 - Select the alternative hypothesis (left-tailed / right-tailed / two-tailed) Step 3 - Enter the level of significance $\alpha$
Step 2 - Enter the sample standard deviations for first sample $s_1$ and second sample $s_2$ Step 1 - Enter the sample size for first sample $n_1$ and second sample $n_2$ Two tailed Calculate Results Test Statistics F: Degrees of Freedom: (df1) Degrees of Freedom: (df2) F-critical value(s): p-value: How to use F test calculator for two variances? F test Calculator for two variances Sample 1 Sample 2 Sample Size Standard Deviation Level of Significance ($\alpha$) Tail Left tailed


 0 kommentar(er)
0 kommentar(er)
